# 分治法

# 概念

什麼是分而治之法？

針對一個有 n 筆輸入的問題，它的策略是把輸入分解成 k (1< k ≤ n) 個獨立的小集合，這導致原問題變成 k 個小問題。
小問題各自獨立地解決後產生各自的解，一共有 k 組解。
分而治之法最後必須將這 k 組解有系統地合併以產生原問題的解。

# 步驟

如果要處理的資料量已經夠少，那麼用直接的方式解決，否則，把輸入資料分解成兩個獨立的小集合
求出每一個小問題的解；並且
把這兩個小問題的解組合起來，成為原來的大問題的解。

以下有範例演示喔～～

# 例題

# d219: 00374 - Big Mod

# 內容

計算 R = B^P mod M
對相當大的 B、P、M 請寫一個有效率的演算法來。

# 思路

$(A\ast B)\%C=(A\%C)\ast(B\%C)\rightarrow B^P\;\%\;M=(B^{P/2\;}\%\;M)\ast(B^{P/2}\;\%\;M)$

不斷往下切的同時，請務必記住，如果 P 是奇數要再多乘一個 B 喔！！！

	#include <bits/stdc++.h>
	using namespace std;

	long long dc(long long b,long long p,long long m)
	{
	if (p==0)
	return 1;
	else if (p==1)
	return b%m;
	else
	{
	long long half =dc ( b , p/2, m);
	if (p%2==0)
	return half * half % m;
	else
	return half * half * b % m;
	}
	}

	int main(){
	long long b,p,m;
	while(cin >> b >> p >> m)
	cout << dc(b,p,m) << endl;
	return 0;
	}

# a233: 排序法～～～挑戰極限

# 內容

排序，就對了

# 思路

難得有機會，來用一下 merge sort 吧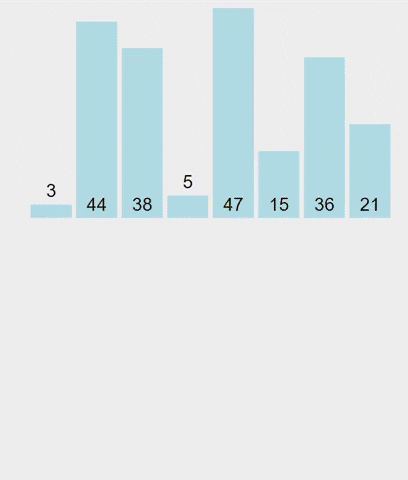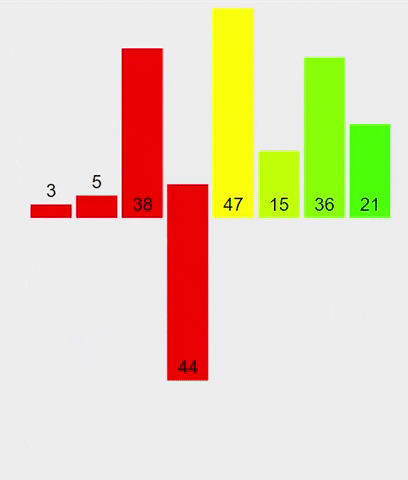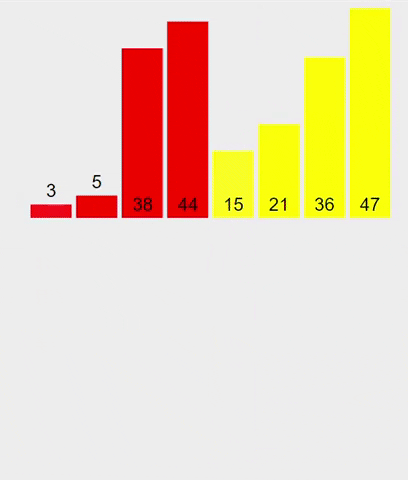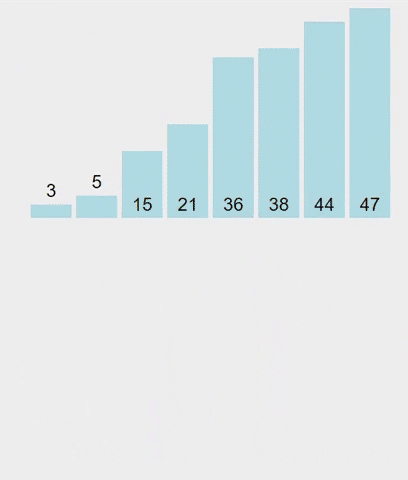
排序囉
如圖所示:

申請空間，使其大小為兩個已經排序序列之和，該空間用來存放合併後的序列；
設定兩個指標，最初位置分別為兩個已經排序序列的起始位置；
比較兩個指標所指向的元素，選擇相對小的元素放入到合併空間，並移動指標到下一位置；
重複步驟 3 直到某一指標達到序列尾；
將另一序列剩下的所有元素直接複製到合併序列尾。

# 程式碼

	#include<iostream>
	using namespace std;
	// 合併時需要兩個子陣列
	// 第一個是紀錄 arr [l..m]
	// 第二個是紀錄 arr [m+1..r]
	void merge(int arr[], int l, int m, int r)
	{
	int i, j, k;
	int n1 = m - l + 1;
	int n2 = r - m;
	int L[n1], R[n2];

	/* 將數值複製過去 L [] and R [] */
	for (i = 0; i < n1; i++)
	L[i] = arr[l + i];
	for (j = 0; j < n2; j++)
	R[j] = arr[m + 1 + j];

	/* 合併這兩者到 arr [l..r] 中 */
	i = 0; // 定義第一個的 index
	j = 0; // 定義第二個的 index
	k = l; // 定義被合併的 index
	while (i < n1 && j < n2) {
	if (L[i] <= R[j]) {
	arr[k] = L[i];
	i++;
	}
	else {
	arr[k] = R[j];
	j++;
	}
	k++;
	}

	/* 將剩餘的 L [] 複製過去 */
	while (i < n1) {
	arr[k] = L[i];
	i++;
	k++;
	}

	/* 將剩餘的 R [] 複製過去 */
	while (j < n2) {
	arr[k] = R[j];
	j++;
	k++;
	}
	}

	void mergeSort(int arr[], int l, int r)
	{
	if (l < r) {

	int m = l + (r - l) / 2;
	// 將排序分成二部分
	mergeSort(arr, l, m);
	mergeSort(arr, m + 1, r);
	// 整合
	merge(arr, l, m, r);
	}
	}

	int main()
	{
	int n; cin>>n;
	for(int i = 0;i<n;i++)
	cout<<arr[i]<<" ";
	mergeSort(arr, 0, n-1);

	for(int i = 0;i<n;i++)
	cout<<arr[i]<<" ";
	return 0;
	}

# b373: [福州 19 中] 车厢重组

# 內容

在一个旧式的火车站旁边有一座桥，其桥面可以绕河中心的桥墩水平旋转。一个车站的职工发现桥的长度最多能容纳两节车厢，如果将桥旋转 180 度，则可以把相邻两节车厢的位置交换，用这种方法可以重新排列车厢的顺序。于是他就负责用这座桥将进站的车厢按车厢号从小到大排列。他退休后，火车站决定将这一工作自动化，其中一项重要的工作是编一个程序，输入初始的车厢顺序，计算最少用多少步就能将车厢排序。车厢编号从 1 开始。

其實，就是指說：給你一串數列，問最少交換幾次可以使號碼由小而大排好

# 思路

其實，它就是十分經典的問題之一喔～，稱作 – 逆序數對數量計算
對於一個陣列 A 中，任取兩個元素，順序不變，如果前者大於後者，則我們稱為逆序數對
其解決方法有三，一為暴力法，二為分治法，三為 BIT 解法，在這就先用分治法吧

經過觀察會發現:

即使將左右兩部分排序，這部分的數量依然相同～～(廢話)~~
經過排序以後窮舉左邊的每一項，與它有關的逆序數對是原本右邊滿足的部分，加上往右找比它小的那些數值

# 作法

以合併排序法為基礎
在合併前額外加上計算 “橫跨左右部分的逆序數對數量”
回傳三個部份的總和，就是在處理範圍中的逆序數對數量
順便也幫忙排序完成了！

在此問題中，子問題的答案並不只有「該區間內逆序數對的數量」，也隱含了「該區間內排序過的結果」

# 程式碼

	#include<bits/stdc++.h>
	using namespace std;
	#define N 1000005
	#define int long long
	int data[N],tmp[N];
	int mergecount(int L,int R){
	if(L+1==R) return 0; // 僅有單一元素
	int count=0,M=(R-L)/2+L;
	count+=mergecount(L,M); // 左
	count+=mergecount(M,R); // 右

	int a=L,b=M,k=L,t=M-1;
	for(int i=L,i<M;i++){
	while(t+1<R&&data[i]>data[t+1]) t++;
	count+=t-M+1;
	}
	/* 順便合併排序 */
	while(a<M\|\|b<R){
	if(a<M&&(b>=R\|\|data[a]<data[b])){
	tmp[k++]=data[a++];
	}else{
	tmp[k++]=data[b++];
	}
	}

	for(int i=L,i<R,i++) // 儲存合併排序的結果
	data[i]=tmp[i];
	return count;
	}
	int main(){
	ios::sync_with_stdio(false);
	cin.tie();
	int n,ans,t=1;
	while(cin>>n&&n){
	for(int i=0;i<n;i++)
	cin>>data[i];
	ans=mergecount(0,n);
	cout<<ans;
	}
	return 0;
	}

C++ 自主學習程式語言筆記

# 分治法

# 概念

# 步驟

# 例題

# d219: 00374 - Big Mod

# 內容

# 思路

# a233: 排序法～～～挑戰極限

# 內容

# 思路

# 程式碼

# b373: [福州 19 中] 车厢重组

# 內容

# 思路

# 作法

# 程式碼

第11課、模擬

d663: 11730 - Number Transformation