# DFS

# 想法

深度優先搜尋法（Depth-First Search）是一種樹（Tree）或圖（Graph）資料結構的搜索演算法，從圖的某一節點 (vertex, node) 開始走訪，盡可能最深入到分支深處再回溯其他節點。可應用於有向圖與無向圖的搜尋。

# 動圖演示

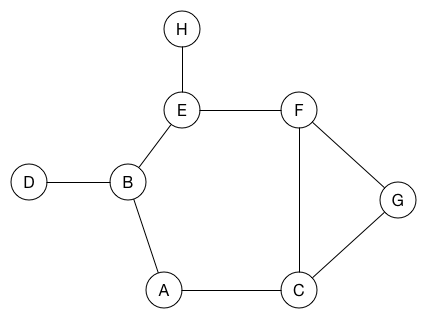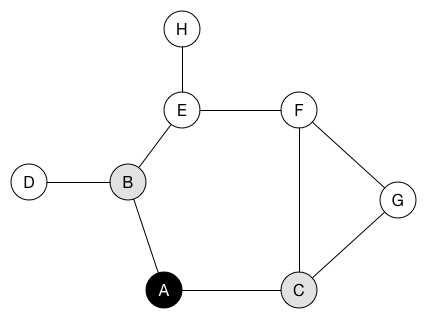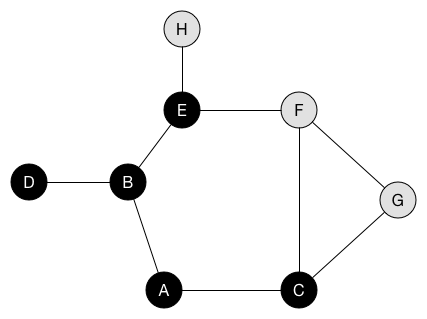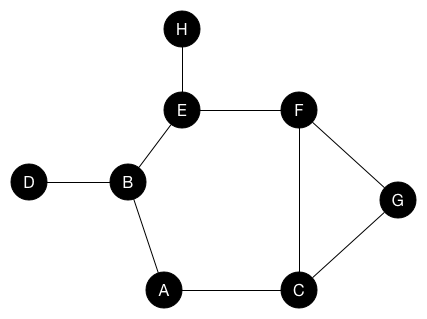
# 方法

運用遞迴的方式，不斷的往合理的狀況往下探索，直到無法在往下探索後返回，直到把所有狀況都跑過一遍，有時需要用到 stack 去幫忙輔助。

# 用途

用於拓撲排序，解決需要圖形回溯的問題，檢測圖形中的循環，查找兩個節點之間的所有路徑等。當然，還有很多喔～～

# tree search backtracking

許多問題尋找解答的過程可以表示成樹，建構出解答空間樹 (solution space tree)，因此找解答就轉變成一個樹搜尋問題。
DFS vs. 回溯 (backtracking)
- DFS 會遍訪每一個未拜訪過的節點，如果該節點已無可拜訪的節點，就會退回該節點的父節點再遍訪其它分支的節點。
- backtracking 在進行未拜訪節點選擇時，可以先選擇可能會有好結果的分支，或是提早判斷若無解，就不遞迴至下一層，而是回溯退回先前的節點。(偷吃步)

# 上課例題

# d908: 4. 最佳路徑

在以有向圖中的某一個節點做為起始節點的所有可能路徑中，計算其中擁有最大權重總和的路徑之權重總和值為多少？
PS. 我們假設在此討論的有向圖都不會存在有一條路徑的起始節點與終止節點是同一個。

運用 DFS 從頭 (0) 向相鄰節點往下探尋，直到無其餘相鄰後再進行回溯，直至跑完全圖。

	#include <bits/stdc++.h>
	using namespace std ;
	int maxx,n,d;
	char s,a,b;
	int Map[26][26]={},used[26]={};

	void dfs(int c, int sum) {
	maxx = max(maxx,sum);
	for(int i = 0;i<26;i++){
	if(!used[i]&&Map[c][i]){
	used[i] = 1;
	dfs(i, sum+Map[c][i]);
	used[i] = 0; // 回溯
	}
	}
	}

	int main() {
	cin>>s>>n;
	for(int i = 0;i<n;i++){
	cin>>a>>b>>d;
	Map[a-'A'][b-'A'] = max(Map[a-'A'][b-'A'],d);
	}
	maxx = 0;
	dfs(s-'A',0);
	cout << maxx<<endl;
	}

# d324: 00750 - 8 Queens Chess Problem

在西洋棋得棋盤中你可以放置 8 個皇后而且彼此都不衝突（就是都不能吃到對方）。
給你某一個皇后的位置，請你寫一個程式來輸出所有這樣可能的安排。

運用 DFS 嘗試將每個皇后放在可能正確的位置上。
若在放完全部棋子之前就檢測到不合理的存在就回到上一顆重新放置，直至放置完成為止。

	#include<bits/stdc++.h>
	using namespace std;

	int queen[9];
	int ans;
	void walk(int);

	int main(){
	int n; cin>>n;
	while(n--){
	int x,y; ans=0;
	cin>>x>>y;
	memset(queen,-1,sizeof(queen));
	queen[y]=x;
	cout<<"SOLN COLUMN\n # 1 2 3 4 5 6 7 8\n\n";
	walk(1);
	}
	}

	bool check(int floor){
	for(int i=1;i<floor;i++){
	if(queen[i]==queen[floor]) return false;
	if(queen[floor]-queen[i]==floor-i) return false;
	if(queen[floor]-queen[i]==i-floor)return false;
	}
	return true;
	}

	void walk(int floor){
	if(floor==9){
	printf("%2d ",++ans);
	for(int i=1;i<=8;i++)
	cout<<queen[i]<<" ";
	cout<<endl; return;
	}
	if(queen[floor]>0) {
	if(check(floor)) walk(floor+1);
	}
	else{
	for(int i=1;i<=8;i++){
	queen[floor]=i;
	if(check(floor))walk(floor+1);
	queen[floor]=-1;
	}
	}
	}

# c812: 1. 觀光景點

圖上有 $N$ 個點，分別以 $\{V_1, V_2, …, V_N$ 代表觀光點，並精心挑選了 $N-1$ 組觀光點以線段相連並依據經驗給定 $R(i,j)$ 值，以代表 $V_i$ 與 $V_j$ 的相關性。特別的是，該圖之任意兩點 Vm 與 Vn 一定有單一路徑 p ，相互串連，而 $V_m$ 與 $V_n$ 的相關性就為該路徑上所有已知相關性的最小值 $R(i,j)$

DFS

	#include <bits/stdc++.h>
	using namespace std;

	vector< pair<int,int> > g[5005];
	bool vst[5005]={0};
	int q,ans=0;

	void dfs(int now,int r){
	vst[now] = true;
	if(r>=q)
	ans++;

	for (auto nxt : g[now])
	if (!vst[nxt.first])
	dfs(nxt.first,min(nxt.second,r));
	}

	int main(){
	int n,vk,i,j,w;
	cin >> n >> vk >> q;
	for(int t=0;t<n-1;t++){
	cin >> i >> j >> w;
	g[i].push_back({j,w});
	g[j].push_back({i,w});
	}

	dfs(vk,0x3f3f3f3f);
	cout << ans-1 << endl;

	return 0;
	}

# 延伸練習

# d626: 小畫家真好用

小畫家裡面有一種繪圖工具，叫做油漆桶工具，只要選定你要的顏色、油漆的地點就可以進行填色
油漆桶的填色範圍是取決於 "同色塊相鄰" 的原則，現在請你模擬這項工具

從點擊的那點開始向四方向擴散，直至四方向都已著上顏色為止。

	#include <bits/stdc++.h>
	using namespace std;

	char mp[110][110];
	char inp[102];

	void dfs(int i,int j) {
	if(mp[i][j]=='+')
	return;

	mp[i][j]='+';
	dfs(i,j+1);
	dfs(i+1,j);
	dfs(i,j-1);
	dfs(i-1,j);
	}

	int main(){
	int a;
	while(scanf("%d",&a)!=EOF) {
	memset(mp,'+',sizeof(mp));
	int i,j;
	for(i=1;i<=a;i++){
	scanf("%s",inp);

	for(j=1;j<=a;j++)
	mp[i][j]=inp[j-1];

	int n,m;
	scanf("%d%d",&n,&m);
	dfs(n+1,m+1);
	for(i=1;i<=a;i++){
	for(j=1;j<=a;j++)
	cout<<mp[i][j];
	cout<<endl;
	}
	}
	return 0;
	}

# a290: 新手訓練系列～圖論

給一個有向圖，如果 A 城市可以到達 B 城市，請輸出 Yes!!! 不行請輸出 No!!!

使用 DFS 從 A 開始向相鄰處尋找，直至無法前進為止。
如果 A 城市可以到達 B 城市，請輸出 Yes!!! 不行請輸出 No!!!

	#include<bits/stdc++.h>
	using namespace std;

	vector<int> v[802];
	bool found[802],able=false;

	void dfs(int from,int to){
	if(from==to) {
	able=true;
	return;
	}
	for(int i=0;i<v[from].size();i++)
	if(v[from][i]==to) {
	able=true;
	return;
	}
	else if(!found[v[from][i]]) {
	found[v[from][i]]=true;
	dfs(v[from][i],to);
	}
	}

	int main(){
	for(int N,M,A,B;scanf("%d %d",&N,&M)!=EOF;able=false)
	{
	memset(found,false,sizeof(found));
	for(int i=0;i<802;v[i].clear(),i++);

	for(int i=0,a,b;i<M&&scanf("%d %d",&a,&b)!=EOF;v[a].push_back(b),i++);
	scanf("%d %d",&A,&B);
	dfs(A,B);
	printf((able?"Yes!!!\n":"No!!!\n"));
	}
	return 0;
	}

# b967: 第 4 題血緣關係

0 是 7 的孩子， 1、2 和 3 是 0 的孩子， 4 和 5 是 1 的孩子， 6 是 3 的孩子。
我們可以輕易的發現最遠的親戚關係為 4 (或 5) 和 6 ，他們的 "血緣距離" 是 4 (4→1→0→3→6)。

給予任一家族的關係圖，請找出最遠的 "血緣距離"。
你可以假設只有一個人是整個家族成員的祖先，而且沒有兩個成員有同樣的小孩。

先任意尋找一沒有小孩的點作為尋找點 (root)，再尋找距離它最遠的點，並隨時記錄過程中經過的最遠點距離，直至搜尋完成後，再輸出最大的那一距離。

	#include<bits/stdc++.h>
	#define MAX 100001
	using namespace std;

	vector <int> F[MAX];
	int md;
	int a, b,root,rd,n;
	bool isChild[MAX];

	int DFS( int x ) {
	int max1, max2, result;
	if (F[x].empty()) return 0;
	if (F[x].size() == 1) return DFS(F[x][0])+1;
	int times = 1;
	for (auto child : F[x]) {
	result = DFS(child) + 1;
	if (times == 1) max1 = result;
	else if (times == 2) {
	if (max1 >= result) max2 = result;
	else {
	max2 = max1;
	max1 = result;
	}
	} else {
	if (max1 <= result) {
	max2 = max1;
	max1 = result;
	}
	else if (max2 < result)
	max2 = result;
	}
	times++;
	}
	md = max(md, max1 + max2);
	return max1;
	}

	void init(){
	md = 0;
	for (int i = 0; i<n; i++) {
	F[i].clear();
	isChild[i] = false;
	}
	for (int i = 1; i<n; i++) {
	cin>>a>>b;
	F[a].push_back(b);
	isChild[b] = true;
	}
	}

	int find_root(){
	for (int i = 0; i < n; i++)
	if (!isChild[i]) return i;
	}

	int main() {
	ios::sync_with_stdio(false);cin.tie(0);
	while (cin>>n) {
	init();
	root = find_root();
	rd = DFS(root);
	cout<< max(md,rd)<<endl;
	}
	}