第 01 篇、基本數學 - 離散數學 - 自修課程 (大學)

# 集合論 `set`

集合 set 為一堆物品的收集

# 定義

$x \in A \leftrightarrow x$ 為 $A$ 的元素
$|A|$ 表示 $A$ 的元素個數，稱作 $A$ 的基數
$A \subseteq B \leftrightarrow ( \forall x \in A \rightarrow x \in B)$
$A \subset B \leftrightarrow (A \subseteq B \wedge A \neq B)$
$A=B \leftrightarrow (A \subseteq B \wedge B \subseteq A)$
$\phi$ 表示空集合

note

$| \phi | = 0, |\{ \phi \}| = 1$
$\phi \subseteq A$ (空集合是任何集合的子集合)

# 常見數系

$\mathbb{N} = \{ 0, 1, 2, 3,...\}$ 自然數
$\mathbb{Z} = \{ ...,-2,-1,0,1,2,...\}$ 整數
$\mathbb{Z}^{+} = \{ 1,2,3,4... \}$ 正整數
$\mathbb{Q} = \{ \frac{q}{p} |p,q \in \mathbb{Z}, p \neq 0 \}$ 有理數 (循環小數)
$\mathbb{R}$ 實數
$\overline{\mathbb{Q}}$ 無理數
$\mathbb{C}$ 複數

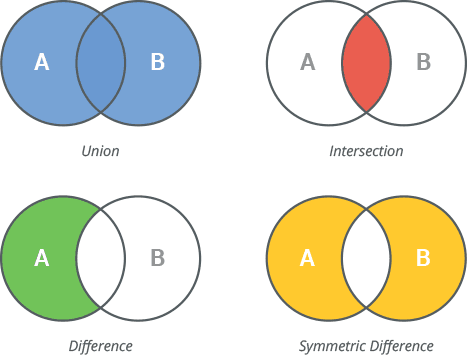
# 運算

聯集 union : $A \cup B = \{ x | x \in A \cup x \in B \}.$
交集 intersection : $A \cap B = \{ x | x \in A \cap x \in B \}.$
差集 difference : $A-B = \{ x| x \in A \cap x \notin B \}.$
補集 complement : $\overline{A} = \{ x | x \notin A \}.$
對稱差 symmetric difference : $A\oplus B = (A \cup B) - (A \cap B)$

示意圖

# 性質

# 交換性

$A \cap B = B \cap A$
$A \cup B = B \cup A$
$A \oplus B = B \oplus A$

# 結合性 (相同運算)

$(A\cup B) \cup C = A \cup ( B \cup C)$
$(A\cap B) \cap C = A \cap ( B \cap C)$
$(A\oplus B) \oplus C = A \oplus ( B \oplus C)$

# 分配性 (不同運算)

$A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$
$A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$
$A \cap (B \oplus C) = (A \cap B) \oplus (A \cap C)$ (交集有分配性)
$A \cup (B \oplus C) = (A \cup B) \oplus (A \cup C)$ (聯集無分配性)

# 迪摩根定理

$\overline{A \cup B} = \overline{A} \cap \overline{B}$
$\overline{A \cap B} = \overline{A} \cup \overline{B}$

# 逆集合

# 卡氏積

令 $A$ 、 $B$ 皆為一集合，定義 $A \times B = \{ (a,b)| a\in A , b \in B \}$ 稱為 $A,B$ 的卡氏積

note

$|A| = m, |B| = n \Rightarrow |A \times B| = m \times n$
$A_1 \times A_2 \times ... \times A_n = \{ (a_1,a_2,...,a_n) | a_1 \in A_1, a_2 \in A_2 \}.$
$\mathbb{R} \times \mathbb{R} = \mathbb{R^2} = \{ (a,b) | a,b \in \mathbb{R} \}$
$\mathbb{R^n} = \underset{n}{\underbrace{\mathbb{R} \times \mathbb{R} \times ... \times \mathbb{R}}}$

# 數學歸納法

# 定理

令 $P(n)$ 為一命題，且 $n \in \mathbb{Z^{+}}$

Basic Step : $P(1) = true$
Inductive Step : 設 $P(k) = true$ 推導 $P(k+1) = true$
則， $P(n) = true, \forall n \in \mathbb{Z^{+}}$

良序性公設

$A \subseteq \mathbb{Z^{+}},A \neq \phi$ ，則 $A$ 中存在最小元素 (正整數最小是 1)

# 基本數論 (整數)

# 質數 `prime`

# 定義

若 $n(n \geq 2)$ 除了 1 及 $n$ 外無其他正因數，
稱 $n$ 為一質數 prime ，否則 $n$ 為組合數 composite

小補充

$|$ 表示整除，例如: $2|6 , 3|9 , 2|0$

# 定理

$\mathbb{Z^{+}}$ 中質數個數為 $\infty$

note

$n = P_1^{e_1}P_2^{e_2}P_3^{e_3}...P_k^{e_k}.$

$n$ 的正因數個數為 (e_1+1)(e_2+1)...(e_k+1)
Euler's totient function: $\varphi(n) = n \prod_{\substack{ p | n \\ }} \left( 1 - \dfrac{1}{p} \right)$ 表示 $1~n$ 之中與 $n$ 互質的個數

# 定理

$m = nq + r \rightarrow gcd(m,n) = gcd(n,r)$ 輾轉相除法

note1

$gcd(n,n+1) = gcd(n,n+1) = 1$ 兩數相鄰必定互質

note2

$gcd(a,b) = g$ 時，

$\{ as+bt| s,t \in \mathbb{Z} \} = \{ gz | z \in Z \}.$
$ax+by = c$ 有整數解 $\Longleftrightarrow g|c$
可運用輾轉相除法，求出 $x,y$

# 定義

$a \equiv b(\bmod n) \leftrightarrow n | (a-b)$ 可想成 $(a-b)$ 為 $n$ 的倍數

判斷題

$a \equiv b (\bmod n) \rightarrow 2a \equiv 2b (\bmod n)$
$a \equiv b (\bmod 2n) \rightarrow a \equiv b (\bmod n)$
$a \equiv b (\bmod 2n) \rightarrow 2a \equiv 2b (\bmod 2n)$
$a \equiv b (\bmod n) \rightarrow a \equiv b (\bmod 2n)$
$ka \equiv kb (\bmod n) \rightarrow 2a \equiv 2b (\bmod n)$
這是一個小 bug

note

$a \equiv b (\bmod n), c \equiv d (\bmod n)$
$a+c \equiv b + d (\bmod n)$
$2a \equiv 2b (\bmod n)$
$ka \equiv kb (\bmod n)$
$ka \equiv kb (\bmod n) \nRightarrow a \equiv b (\bmod n)$
需 $gcd(k,n) = 1$

# 乘法反元素 `Inverse`

# 定義

$gcd(a,n) = 1$ ，若 $ab \equiv 1(\bmod n)$
稱 $b$ 為 $a$ 的 inverse ，記作 $a^{-1}(\bmod n)$

# 費馬小定理 `Fermat's little theorem`

令 $p$ 為一質數， $a$ 為一整數，若 $a$ 不是 $p$ 的倍數，則
$a^{p-1} \equiv 1 (\bmod p)$

# 定理

$gcd(a,n) = 1 \Rightarrow a^{\varphi(n)} \equiv 1(\bmod n)$

# 中國餘數定理 `Chinese Remainder Theorem`

$n_1,n_2,...,n_k \in \mathbb{Z^+}$ 彼此互質，希望乘法反元素存在
$r_1, r_2,...,r_k \in \mathbb{Z}$
$n = n_1 \times n_2 \times ... \times n_k$
則: $\left\{ \begin{array}{cl} x \equiv r_1 (\bmod n_1) \\ x \equiv r_2 (\bmod n_2) \\ ....\\ x \equiv r_k (\bmod n_k) \\ \end{array} \right.$ 在 $\bmod(n)$ 下必有解

數學大學自修離散數學

# 集合論 set

# 定義

# 常見數系

# 運算

# 性質

# 交換性

# 結合性 (相同運算)

# 分配性 (不同運算)

# 迪摩根定理

# 逆集合

# 卡氏積

# 數學歸納法

# 定理

# 基本數論 (整數)

# 質數 prime

# 定義

# 定理

# 定理

# 定義

# 乘法反元素 Inverse

# 定義

# 費馬小定理 Fermat's little theorem

# 定理

# 中國餘數定理 Chinese Remainder Theorem

火苗還在燃燒

第02篇、關係

# 集合論 `set`

# 質數 `prime`

# 乘法反元素 `Inverse`

# 費馬小定理 `Fermat's little theorem`

# 中國餘數定理 `Chinese Remainder Theorem`