題目連結: https://tioj.ck.tp.edu.tw/problems/1040
# 內容
連分數有許多不為人知的應用,一開始一位印度數學家利用連分數解出了 ax+by=c 的一次不定方程式,連分數還跟我們日常生活中的曆法有密切的關係,那什麼是連分數呢?
連分數一般如下面形式: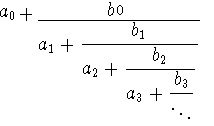
連分數有四種,一種是無窮連分數可以一直延展下去,一種是有窮連分數,而連分數又可分為簡單連分數,即分子部份永遠是 1 ,另一種是非簡單連分數,分子部份是由其他數字所組成。每一個有理數都可以用簡單有窮連分數來表示:
簡單有窮連分數不會一直延展下去,當子分數的分母為一整數時,就要停止。
現在輸入 P 和 Q,請你幫忙將 P/Q 化為連分數吧。
# 思路
每一次就是分成 a/b + a% b,而下一次再拆解時則 a = b,b = a% b,不斷往下走
是不是有點像輾轉相除法阿
# 程式碼
#include <cstdio> | |
#include <cstdlib> | |
void dfs(int a, int b){ | |
if(a%b == 0){ | |
printf("%d", a/b); | |
return; | |
} | |
printf("%d+1/",a/b); | |
if(b%(a%b) != 0) printf("{"); | |
dfs(b, a%b); | |
if(b%(a%b) != 0) printf("}"); | |
return; | |
} | |
int main(){ | |
int T; scanf("%d", &T); | |
while(T--){ | |
int a, b; | |
scanf("%d %d", &a, &b); | |
printf("%d/%d = ", a, b); | |
dfs(a, b); | |
puts(""); | |
} | |
return 0; | |
} |